Computer Graphic (CG) Semester 4 (Revised Course) (3 Hours) May 2009

Computer Graphic (CG) Semester 4 (Revised Course) (3 Hours) May 2009
VR-3780 [Total Marks : 100]
N.B:	(1)	Questions no 1 is compulsory.
	(2)	Attempt any four questions out of remaining six questions.
	(3)	Assume suitable data if necessary and justify the same
	(4)	Figures to the right indicate full marks.
	(5)	Programming language can be C/C++/JAVA.
1.	(a)	Explain Cyrus-Beck line clipping algorithm and solve the following example using it. Windows is specified by following polygon ABCDE and line to be clipped is P1 P2. A(75, 100), B(150, 75), C(100,50), D(50, 50), E(25, 75), P1(25, 50), P2(150, 75). Calculate P1' and P2'. Note that figure is not to the scale.	08
	(b)	Explain Display File Structure. How one can enter polygon into display file.	05
	(c)	Explain even-odd test to determine whether the point is inside or outside of polygon.	05
2.	(a)	What is window? What is viewport? Assume window and viewport are rectangular. Derive the formulas required, for transforming a point (Xw', YW) in a window to point (Xv', Yv) in viewpoint.	08
	(b)	Explain warnock's algorithm used to remove Hidden Surface with example.	12
3.	(a)	Derive 2D transformation matrix, for performing rotation of given point P(X,Y) by angle 0(theta) in anticlockwise direction about origin. Also explain the steps required if rotation has to be carried out about Fixed Point (i.e. pivot point) (XF', YF).	10
	(b)	Explain Bit-map character generation method.	05
	(c)	What is computer Graphic? State various applications of it. (Specify only names).	05
4.	(a)	Explain sutherland-Hodgman Polygon cliping algorithm, with example. What modification is required on it so that it should also work on following figure. (i.e. concave polygon)	12
	(b)	Explain mid-point circle algorithm. In order to support your explanation, show mathematical derrivation.	08
5.	(a)	State mathematical equations for Bezier curves and Bezier Surface. Explain properties of Bezier Curve.	10
	(b)	Compare Boundary fill and Flood fill algorithm. Illustrate one example with diagram where 4-connected approach fails, while 8 connected approach successes.	10
6.	(a)	Derive the transformations for producing perspective projection of an object, in xy plane. (viewing plane) and COP )Center of Projection) co-ordinates are (a, b, c).	12
	(b)	What are fractals? Give classification of Fractals dimension?	08
7.	(a)	What do you mean by segment? What are the various attributes in segment table? State which operations can be done on segment and explain the same.	08
	(b)	Consider the cube shown in the diagram.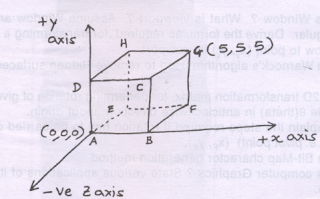 Each side of the cube is 5 units. Co-ordinates of A are (0, 0, 0) co-ordinates of G are (5, 5, 5) In order to perform rotation of cube about the axis joining vertices A and G by angle 45ο in anticlockwise direction, while looking from point G towards origin i.e. pt. A., which transformations are required and specify the matrices for the same.